ここでは推計統計を中心に説明します。推計統計学は全体のデータを調査することができない場合に、抽出(ランダムに選んだ)した標本から全体の状態を推定します。これにより医療の介入や、異なる状況で全体の状況が変化するかを推定するものです。
統計では以下のような基本的な考え方をりようしてデータを分析します(ここでは2群の差を中心に説明します)。
統計は母集団から選んだ標本データを利用して、2つの母集団(例えば男性と女性など)の間の違いがあるかを評価し、その評価に客観性を持たせる(誰が聞いても納得できるもの)にする方法です。
目次
- 母集団と標本 (ランダムサンプリング)
- 計測と尺度
- パラメットリック検定とノンパラメトリック検定
- 対応のあるデータと対応のないデータ
- 計測値の分布 (正規分布=ガウス分布)
- 平均値と分散
- 差の標準化
- 仮説検定:対立仮説と帰無仮説
- 確率の話
1. 母集団と標本 (ランダムサンプリング)
母集団とは、これから検査しようとする対象を含む全ての集団です。男性成人平均寿命などは日本人全ての男性母集団からランダム(無作為)に選んだ標本は母集団と同じ特性を表していると仮定できます。このとき母集団は均一に分布していることが前提とされています。例えば日本の大学1年生と大学4年生の起床時間を調査するとします。大学1年生と大学4年生の起床時間は地域により偏りがない(東京都でも鹿児島県でも同じ)とすると京都の大学1年生と大学4年生の起床時間を調べることで、日本の大学1年生と大学4年生の起床時間を比較できるとします。たとえば九州と北海道では日の出に時間差があり起床時間がずれる要因があればこの仮定は成立しません。従って日の出の時間に差が小さい「近畿圏内の大学1年生と大学4年生の起床時間の比較」の調査は可能と考えられます(日の出の時間要因意以外もかんがえれば)。
下の図はミニトマトを広げた図と思ってください。左側(a)はすべて同じ大きさ、右側(b)は大きいのや小さいトマトが混じっています。平均的な大きさより大きいものや小さい者は少なくなる傾向にあります。
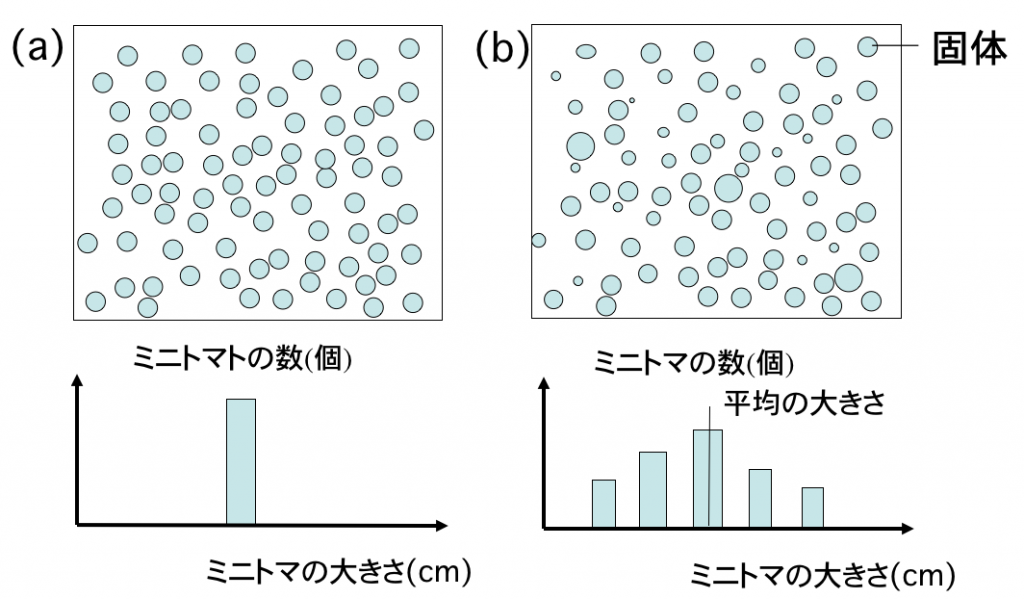
標本(サンプリング):母集団の中からランダムに選んだ値(ランダムサンプリング)の集団を標本と呼びます。この標本に偏りがなければ母集団と同じ分布をもちます。
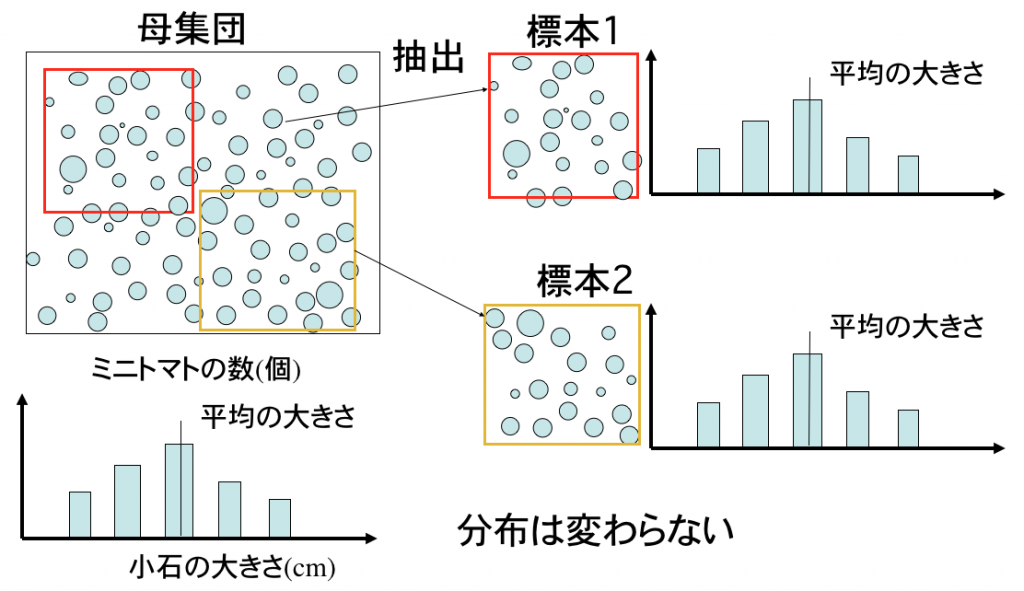
標本抽
・母集団全体を調査することもあります(全数調査)。国勢調査などがこれにあたります。一方標本を調査する方法が標本調査です。
・ランダムサンプリングのランダム(無作為)は「でたらめ」ではありません。年齢や住居などが偏らないように工夫する必要があります(参考:無作為抽出(wikipedia),東京都の統計, NHKが世論調査-NHK放送文化研究所)
2. 計測と尺度
集めるデータにはいろいろなタイプがあります。例えば、体重、体温、痛み感覚、日常生活に関するアンケートなどがあります。
体重計や体温計は等間隔のメモリを持っています。それに対して痛みなど主観的な感覚を計測するためには1-5番などの数字や、どのくらい痛みを感じているのかを指示して0-10cm(0は痛くない10は経験したなかで最高の痛み)などのスケールに表示させることがあります。また、生活に関するアンケートでは「散歩をしますか」などの項目に対して2段階、もしくは4段階で回答するなどのデータがあります。
これらのデータは以下のように分類されます。
尺度水準:サンプルデータには、名義尺度, 順序尺度、間隔尺度、(比率尺度)などがある。(wikipediaの尺度水準を参照)
名義尺度:名前を対象に割り振ったもので、例としては性別、病名、職業、背番号、系統番号などがあります。
順序尺度:順序には意味がある量であり、一般には順位があります。たとえ計測した値であってもその値そのものを利用はできないがその値の大きい小さいは比較できるような場合です。先のスケールを用いたアンケートはVAS(visual analog scale)とよばれ順序尺度としてりようできます。
間隔尺度:等間隔の目盛りで計測でき、任意の原点があるデータです。カレンダーの日付、温度(℃, °K)などがあり、一対のデータの差の計算や、平均値をとることができます(差に意味がある)。10℃は5℃の2倍ではありません。従って温度は比率が計算できません。
比率尺度(比尺度):間隔尺度のデータうち、ユニークな0点(原点)からの数値として規定できるもので、物理量に多く、質量、長さ、絶対温度などがあります。医学では身長、体重、血圧なども入ります。例として体重は50kgの人と75kgを比べると1.5倍と比率の比較ができます。その他、算術平均(加相平均=一般的な平均)が利用できることや、逆数の和などの調和平均などを利用することができます。(比尺度の統計的特性についてはwikipedia等を参照)
| パラメトリック検定 | ノンパラメトリック検定 | |
|---|---|---|
| 尺度水準 | 間隔尺度,比率尺度 | 名義尺度,順序尺度 |
| *名義尺度,*順序尺度 | ||
| 母集団の分布型 | 正規分布を仮定 | 不問 |
| 等分散の仮定 | ||
| 標本サイズ | 少ないと検出力低下 | 不問 |
3. パラメットリック検定とノンパラメトリック検定
パラメトリック検定(間隔尺度・比率尺度)
パラメトリック検定は平均と分散をパラメータとする検定です。平均と分散を利用するためには、データは間隔尺度や比率尺度で計測される必要があり、また、分散は正規分布に従うことが必要です。
パラメトリック検定にはt検定などが含まれます。2群のパラメトリック検定では表計算ソフトに組み込まれているTTEST関数やFTEST関数を用いて容易に結論を得ることができます。ただし、間隔尺度のデータでも、分散が正規分布に従わないデータの場合はノンパラメトリック検定を選択します。
ノンパラメトリック検定(順序尺度)
アンケートを含む順序尺度や名義尺度の場合、母集団の分布が従う分布の予想が困難な場合にはノンパラメトリック検定が利用されます。ノンパラメトリック検定で、対応のある2群のデータにはウイルコクソン(Wilcoxon)の順位和検定が、対応のない2群にはマンホイットニー(Mann-Whitney)符号順位検定が用いられます。
4. 計測値の分布 (正規分布=ガウス分布)
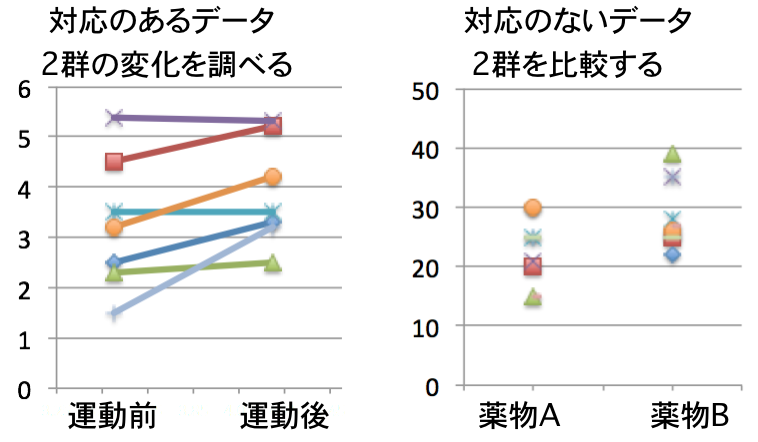
2群の比較を行う研究では同じ被験者から何らかの介入(運動負荷を与える、薬物を投与するなど)の前後でのデータの比較や、異なるグループの状態の比較(AクラスとBクラスの運動機能の比較など)がある。前者が対応のあるデータで後者が対応のないデータとなる。
(a) 対応のあるデータ
・運動負荷による血中乳酸濃度(mg/l)の上昇(同一被験者の運動前後の乳酸濃度データの比較)[パラメトリック検定]
・薬物Aによる最高血圧(mmHg)の変化 (同一被験者のAの投与前後の血圧データの比較)[パラメトリック検定]
・運動負荷による尿のpH変化 (同一被験者のの運動前後での尿のpHを計測(pHは水素イオン濃度の対数)[ノンパラメトリック検定]
・治療介入によるVASで回答した腰痛の変化 (同一被験者で治療前後での腰痛程度の比較) [ノンパラメトリック検定]
(b) 対応のないデータ
・薬物Aと薬物Bの最高血圧(mmHg)の変化 (薬物Aをa群に投与し、薬物Bをb群に投与し、最高血圧の降圧効果(mmHg)を比較した。
5. 平均値と分散
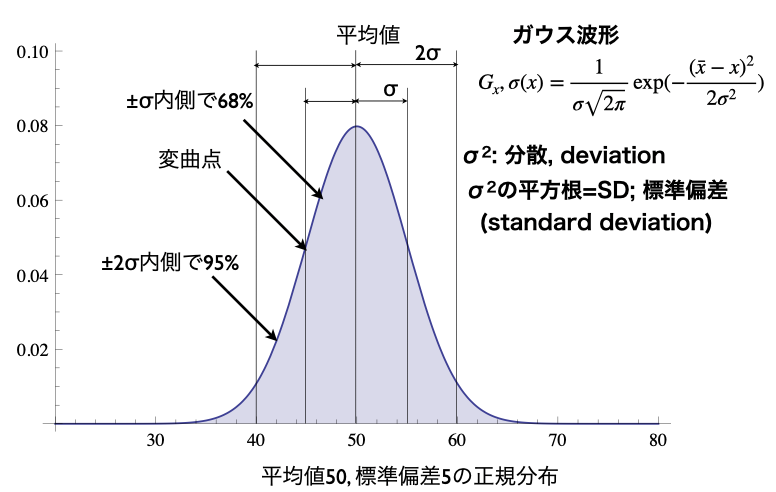
データの分布の形はいろいろあります。たくさんのサンプルがあり、自然な分布ならばガウス分布(正規分布)になります。統計の考えではこのガウス分布になることが基本になっています。ただし、サンプル数や分布の形がガウス分布になっていないこともあります。
ガウス分布の形は以下のようになります。分布は左右対称です。中央値は平均値になり、幅は標準偏差(standard deviation)で表されます。平均値の両側のSD(±SD)の間に全体の68%のデータが入ることになります。2SDの範囲には95%のデータが入ります。
6. 計測と尺度
感覚尺度や比率尺度で計測された正規分布したデータ(パラメトリック検定)は平均値を比較することができます。このとき大事なのはデータのばらつき(分散)の大きさで平均値の差が評価に関連することです。
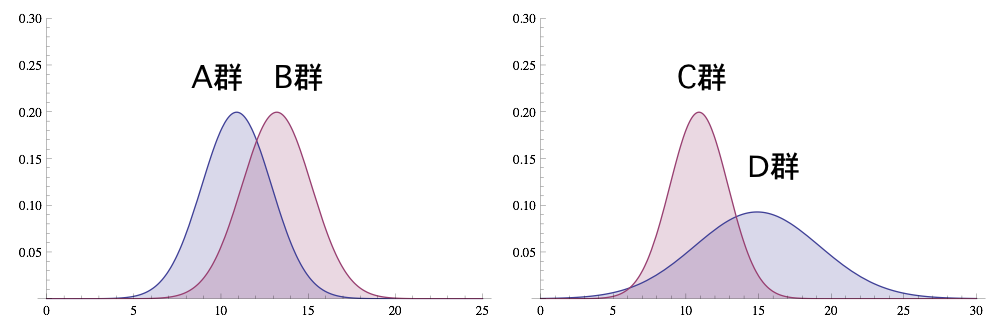
下の図a)は平均値の差に比べて分散が小さく、b)では分散が大きいため同程度の平均値の差がa)に比べてより不確定になります。
また、対応のある検定では、対応するデータ毎に差をとるため、2つのデータ(運動前後など)の分散は等しいと仮定します。
一方、対応のない検定ではデータの分散が等しいときと、分散が等しくないときでは考え方が異なります。分散が等しいかどうかの検定はF検定(後述)を行い判定します。

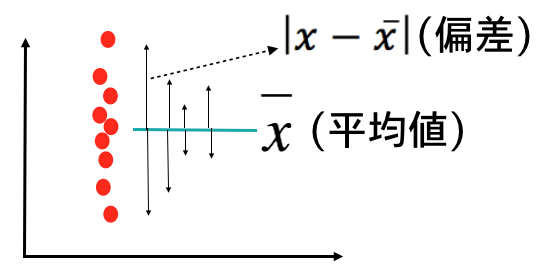
さて、ばらつきは平均値からの各観測データまでの距離の和で表すことができます。この距離の平方和をデータ数で除し(割って)分散を求めます。分散の平方根が標準偏差になります。

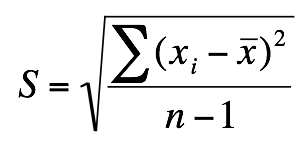
2群の対応のないデータの場合、2つの分散がF検定で評価し等しければ以下のように平均を取ることも可能です。

等分散の検定(F検定)
対応のない2つのデータの分散が等しい(等分散)か不等分散かを調べるにはその標準偏差の比を検定します。このとき分散の大きい方を分母にすることでその比は0−1の間の値をとります。判定はF分布表から有意水準αに対するF値(Fα)を調べ、F置(Fα)とこの比を比較します。Fαより大きいときは、2つの群のデータが同一の正規型母集団から得られたと仮定できます。F検定はFTEST関数を用いて等分散の確率を求めます。
表計算ソフトでは、FTESTの値が0.05より小さければ5%有意水準で等分散の2群となります。
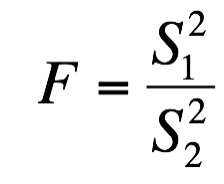
7. 差の標準化
「2群の平均値の差が有意なのかどうか」を判定するために、ばらつきを考慮することにします。このため平均値の差をばらつきで割った値を用いることにします。
ばらつきを示す値としての標準偏差を用いた場合、データ数が多くなる平均値や標準偏差は信頼性が向上します。この効果を考えて標準偏差をデータ数より1少ない値の平方根で割った(データ数が大きいときはデータ数で割る)「標準誤差」をばらつきの指標として利用することでデータ数によらずに差を評価することができます。

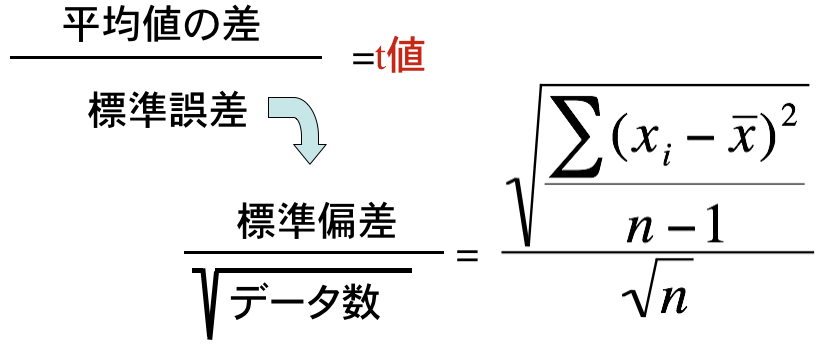
このように標準化した値を統計量と呼びます。この統計量はどのくらいの確率で生じるかが計算されています。2群のパラメトリック検定で得られる統計量はt値です。このt値はt分布表に従います。
次のような対応のある2群の間隔尺度で計測されたデータについて標準化した差を求め、t値を計算すると3.89という値が得られます。
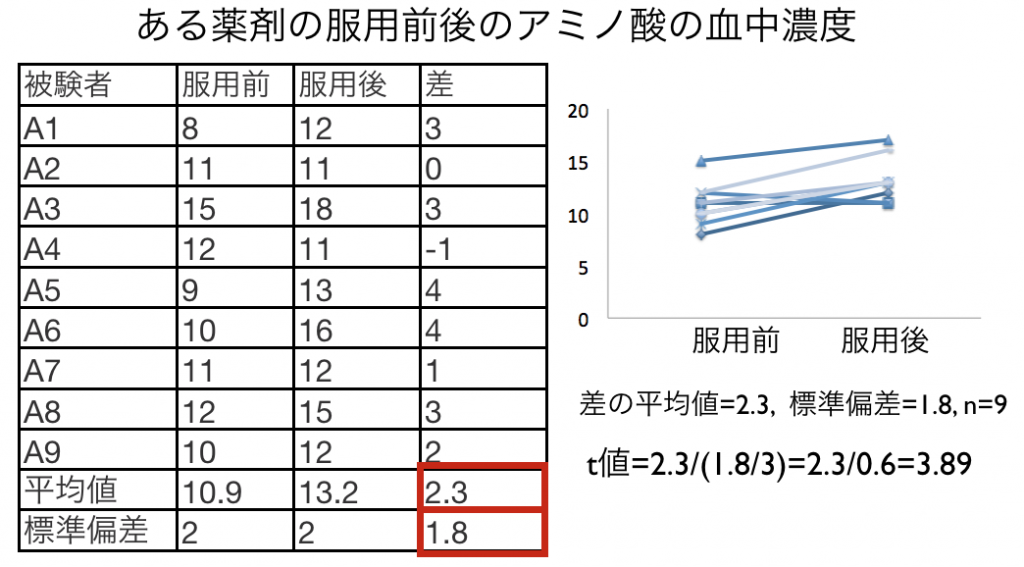
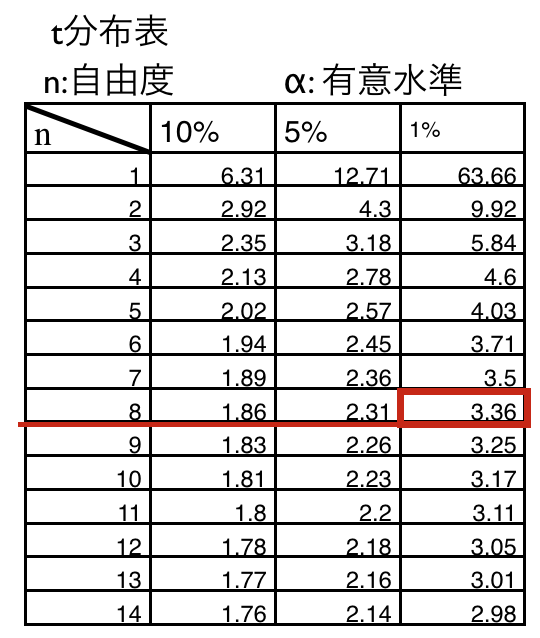
さらに得られたデータ数9から自由度を求めると、対応のある2群の場合は自由度がn-1、つまり8となります。以下のt分布表から自由度nが8の欄をみて、上で得られた値3.89を比較刷ると1%有意水準(3.36)より大きな値を持ちます。
従って、1%有意水準を基準としたときこの標準化された平均値の差が有意に異なる、つまり2群に差があることがわかります。
2群のパラメトリックな検定には一般的にt検定が用いられ、これは表計算ソフトではTTEST関数を用いて計さんされます。
TTEST関数には引数として、「データ1]、「データ2」、2;両側検定、検定の種類(1-3)を指定します。TTEST関数は「2群に差のない確率」を示します。したがって小さい値であれば差があることになります。
対応のない2群ではFTEST関数を用いて2群の分散が等しいかどうかを検定します。
・(1) 対応のある2群の検定の検定の種類は1
対応のない2群の検定の種類は
・(2) FTEST > 0.05 なら 検定の種類は2
・(3) FTEST <= 0.05なら 検定の種類は3
8. 仮説検定:対立仮説と帰無仮説
統計では、仮説検定(Wikipeida)と呼ばれる方法を利用し、2つの母集団から選んだサンプルの間に差があることを示します。正しいことを示すためにその反対のことが滅多に起こらない、つまり確率(下記の項を参照)が低いことからやっぱり正しいとする方法をとります。この反対のことをまず調べようとするのことを帰無仮説といいいます。具体的には次のようになります。
”2つデータが異なる”[対立仮説]を結論としたい
→ ”2つのデータは同じである”[帰無仮説]の確率を計算
→ 確率が低くければ ”2つのデータは同じ”は否定
→ ”2つのデータは異なる”は正しい
ということになります。(統計用語の解説の帰無仮説の項を参照)
例えば明治国際医療大学の学生の男性と女性の数値データの入力速度に差があるかどうかを調べたいと考えます。男女の割合が同数のあるクラスで同じ数値表を入力し速度を計測します。予想では男性と女性で入力速度が差があると考えます(対立仮説)。データを集計して平均値を比較し、2つのデータが同じである(帰無仮説)確率(P:probability)を計算します。確率が小さければ“同じでない”=“速度は男女で異なる”になります。
9.確立の話
統計学という数学を利用して確率で評価を与える。1枚のコインの表のでる確率は0.5ですが、10枚のコインで全て表が出る確率は0.5×0.5×0.5×0.5×0.5×0.5×0.5×0.5×0.5×0.5=0.000976563となります。10枚のコインが同時に表になるのは、10000回投げて7回起こることになります。つまり10枚のコインが表になることは滅多にないことです。つまり確率が低いことになります。仮説検定で計算した確率が小さいと帰無仮説が否定されます。そして対立仮説が正しいこととして認められます。
解説動画:
1.統計用語解説と2群の検定基礎
2. 対応のある検定と対応のない検定