基本的な統計 – 医療情報学

Excelを利用して、2群のt検定など基本的な統計処理について説明します。

1. データのはかり方(尺度水準)とパラメットリック検定とノンパラメトリック検定

データが等間隔および比率尺度のスケール(℃、cmやg, mol/mlなどがあります）で計測されたデータとそうでない(順序尺度と分類尺度)データで分けることができます。
・等間隔(比率尺度を含む)スケール[パラメトリック]：定規のように目盛りが等間隔になっている単位で、mm, Kg, mg/dlなどが比率尺度や、温度や日付などの間隔尺度のデータが含まれます。
これらはパラメトリック検定(統計の考え方を参照)と呼ばれる検定方法で計算されます。

・非等間隔スケール[ノンパラメトリック]：目盛りが等間隔でないスケール(順序、順位)で計測されたデータで痛みの程度などアンケートの分類、VASスケール、フェイススケール、pH（水素イオン濃度指数)、分類などが含まれます。回/分）
ノンパラメトリック検定 と呼ばれる検定方法で計算されます。
ただし、比率尺度・間隔尺度であっても正規性が認められないデータについてはノンパラメトリック検定が利用されます。

2. 群間の対応のある・なし(独立/関連)

次に2つの群のデータ間に対応があるかどうかを考えます。
(a) 対応ありのデータ:主に同一披験者で計測しています。(例:(a)運動前後の血圧の上昇、(b)感冒の治療薬Aの投与前後でののどの痛みの変化など）
(b) 対応なしのデータ：異なる披験者からデータを集めていて、それぞれの群のデータの間に関係がなく、データ数は異なっていてもかまいません。また、同じ被験者でも異なる状態で計測される場合(かなり計測日に隔たりがあり、その人の状態が同じであることが保証されないようなデータを計測する場合など）は対応なしのデータとして取り扱うことが望まれます。（例:(a)男女のある種のタンパク濃度の比較、(b)100ｍダッシュのランニングによる血圧の上昇と100mを自由形で泳いだときの血圧の上昇の比較など。)
対応なしのデータで2群の検定では、2群のデータが等分散かどうかで検定法が異なります。表計算のデータではttest関数の検定の種類が違います。等分散か非等分散かはf検定(ftest)を行い調べます。

3. 2群の検定

パラメトリック検定とノンパラメトリック検定にはそれぞれ対応あり、なしのデータがあり、次のような検定法がよく用いられます。

(a) パラメトリック検定(表計算によるｔ検定:TTEST関数の利用法）
・対応あり：t検定(student t-test)
・対応なし: t検定student t-test) / 等分散の検定 ftest(>0.05; 等分散,　　0.05<非等分散)

(b) ノンパラメトリック検定
・対応あり：Wilcoxonの検定 (表計算ソフトで行うWilcoxsonの検定の方法)
・対応なし：Mann-Whitneyの検定
検定を行った結果は確率Pで示され、Pが0.05以下および0.01の有意水準を指標に、検定の結果を表現します。(参考:
検定の結果の書き方)
*　経時的変化を関数の係数でt検定する
経時的変化の群間比較をするときに、各時点を多重比較する方法がよく採用される。しかし、経時的変化の比較では各時相の比較ではなく全体的な変化を比較したいことあがる。このためには、2群の比較としてその経時的変化に関数をフィットさせ、その係数を2群の比較とするとt検定でその経時的変化の違いを検定することができる。
例としては指数的に減少する数量が5時点で観測された場合、5群の検定とせずに、減少指数関数をフィットして、その時定数をt検定することになります。また、冷却パットを当てたときの体表面の温度を計測した場合の経時的変化は、フェルミ関数をフィットすることで階段的変化を係数として表すことができる。y=a/(exp(x/b)+1)としてa,bの係数を決定する。aは階段の変化の大きさを表すことになる。bとしては変位が1であればbは0.1-0.5程度となる。

4. 多群の比較検定-分散分析

5. カイ二乗検定(wikipedia:カイ二乗検定　 Chi-squared testまたは検定）

カイ二乗検定とは期待値に対する実測値の偏りを調べることに利用できるノンパラメトリック検定法の一つです。ただし、実測値の一つでも5以下の場合はFisher正確検定を利用してください。
「偏りがない」という帰無仮説が正しければ検定統計量がカイ二乗分布に従うような統計学的検定法の総称であるとwikipediaでは定義されています。カイ二乗検定を用いる仮説には、1)期待値に従うかどうか(適合性の検定)、2)独立であるかどうか(独立性の検定)などがあります。
このときの帰無仮説はそれぞれ以下のようになります。
1) 適合性の検定→帰無仮説:データが期待度数分布に等しい
2) 独立性の検定→帰無仮説:方法AとBが独立でない

例としては、得られたデータが期待される分布に従っているかどうかを検定に利用されます。

例1：ある学校の学生から無作為に男女あわせて100人を選んだとき、男女の比率は50人ずつになることが期待されます。この期待通りの比率になっているかを調べる検定がカイ二乗検定です。

例2: 治療Aを評価するのために、年齢を関係なくサンプリングしたとします。このとき治療Aの評価が年齢によって偏っていないかをチェックする場合にも利用できます。この例では以下のような表ができます。(このような表をクロス集計表と呼びます。A11は表計算のセルの番地を示しています)

例題：治療法Aの評価：

	有効	無効	合計
若年層	15	55	70
高齢層	25	25	50
合計	40	80	120

表計算ソフトではCHITEST関数を利用して偏りがない確立を計算します。
CHETEST関数の値が0.05未満（<0.05)であれば、危険率5%で”偏りがある”ことがわかります。

CHITEST関数を利用するには次の手順で行います。
1) 期待値の計算準備(若年:高齢者):　若年者の全体にしめる割合は58.3%(=70/120*100)で、確率は0.583となり、高齢者の全体に占める割合は41.7%(=50/120*100)で、0.417となります。
2) 期待値の計算準備(有効：無効): 有効と答えるのは全体の33%(0.33=40/120), 無効と答える確率は67%(0.67)となります。
3) 若年者期待値の計算 : 若年者で有効と答える期待される人数(期待値)は0.58*0.33*120=23.3人, 若年者で無効と答えると期待される人数(期待値)は0.58*0.67*120=46.7人となります。
＊実際の計算では、若年者で有効は70*40/120=23.3(人)とけいさんできます。

4) 高齢者期待値の計算：　　高齢者で有効と答えると期待される人数(期待値)は0.42*0.33*120=16.7人、高齢者で無効と答えると期待される人数(期待値)は0.42*0.67*120=33.3人です。
*計算では高齢者で有効は40*50/120=16.7(人)と計算できます。

こうして以下の期待値の表が作成されます。

期待値	有効期待値	無効期待値
若年層	23.3	46.7
高齢層	16.7	33.3

→　期待値がわかればカイ二乗検定の帰無仮説に対する確立はCHITEST(B2:C3, B7:C8)で計算されます。
*B2:C3は実際のアンケート結果、B7:C8は期待値の計算結果。

帰無仮説の確立が求められたら、検定の結果のかかきたを参考に結果と結論が掛けます。
*この例では確立は0.001<0.01なので、1%有意水準で有意さがあり、若年者では有効と回答する被験者が21％なのに対し、高齢者では有効(あるいは無効)と解答する被験者が50％です。したがって若年者と高齢者では有効回答に偏りが認められるということになります。

6. 相関係数と回帰直線

相関係数rが有意であるかどうかを検定することができます。
「データの母相関係数σ=0」を帰無仮説H₀としてならばt値は以下の式に従います。得られたt値をt分布表で自由度(n-2)の時の値と比較し、t分布表の値より大きければ有意な相関係数ということになります。

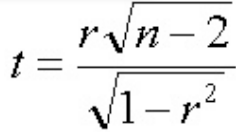
相関係数	-0.35	=CORREL(C3:C17,D3:D17)
自由度	13	=COUNT(C3:C17)-2
t値	1.24	=ABS(G3*(G4-2)^0.5/(1-G3^2)^0.5
p値	0.237	=TDIST(G5,G4,2)

excleでt値を計算したら続いて、TDIST(t値, 自由度(数-2),2(両側))によりP値を計算することができる。

* データは「C3:C17」と「D3:D17」にある
* 相関係数はG3, 自由度はG4, t値はG5にある。
* この例ではp値が0.237>0.05なので相関係数は有意でない。

(2018.6.6)