TTEST関数の使い方と統計の結果の書き方(2群のパラメトリック検定について)
TTEST関数は関連2群または独立2群の正規分布するデータ(標本)の平均値に有意な差があることを検定する関数です。(excelやspreadsheetなどでサポートされています)
関連のない(独立な)2群のデータではそれぞれのデータの分布が等分散か等分散でない(非等分散)のf検定を行う必要があります。
- t検定の帰無仮説は”2群の平均値に差がない”です。 TTESTが0.05未満なら”2群の平均値に差が無い”が否定され、2群に有意な差があるとなります。
- f検定の帰無仮説は”分散が等しい”です。FTEST(データ列A; データ列B)は分散が等しくない確立を計算します。確立が0.05未満であれば”等分散”が否定されて非等分散となり、反対に0.05以上であれば等分散になります。
対応のあるt検定(データが正規分布のとき)
->TTEST(データ列A, データ列B, 2(両側), 1(検定の種類) )
対応のないt検定(FTEST>=0.05; 等分散の2群)
->TTEST(データ列A, データ列B, 2(両側), 2(検定の種類) )
対応のないt検定(FTEST<0.05; 非等分散の2群)
->TTEST(データ列A, データ列B, 2(両側), 3(検定の種類) )
TTEST関数の使用例
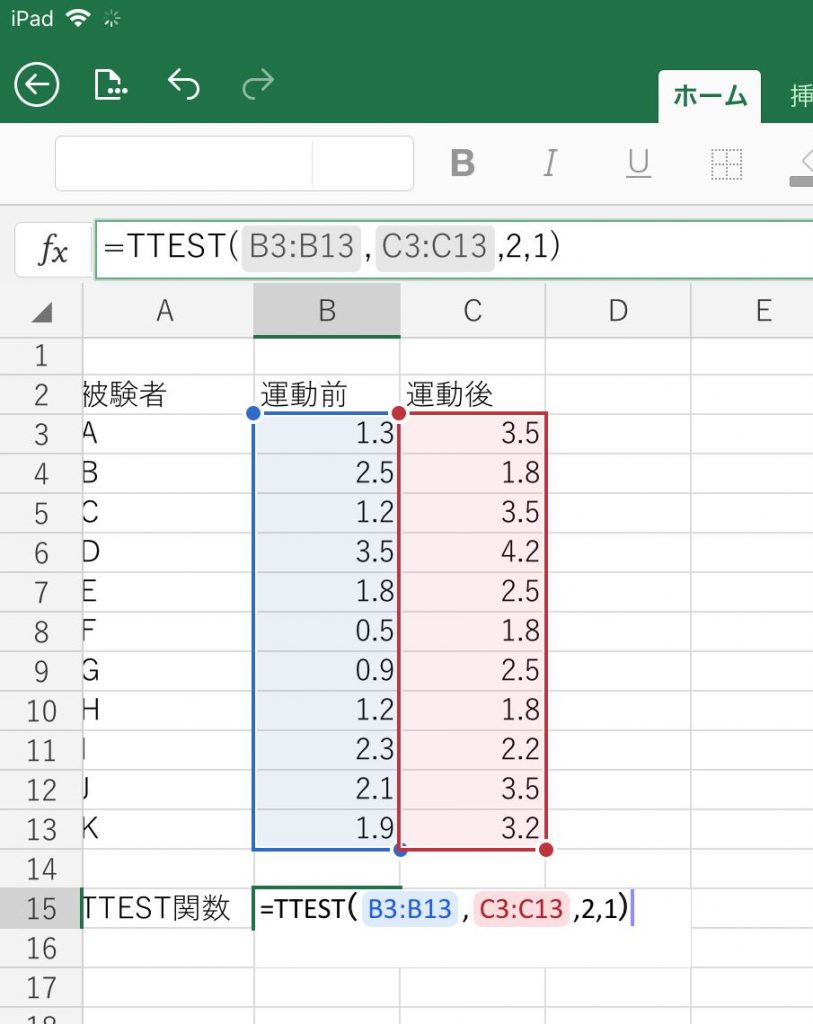
有意差の書き方
TTEST関数の結果が0.05以上(TTEST>=0.05)→ “2群の結果に有意差がない”
TTEST関数の結果が0.05未満(0.05>TTEST>=0.01)→ ” 危険率5%で2群の結果に有意差がある”
TTEST関数の結果が0.01未満(0.01>TTEST)→ “危険率1%で2群の結果に有意差がある”
結論の書き方
有意差がある場合の結論の書き方の例は以下のようになります。
有意水準あるいは危険率5%で2群に差がある場合:「薬剤は有効である」
有意差がなければ「薬剤の効果は認められない」
(その他の例)Aの平均値がBの平均値より大きい場合、”AはBより大きい”と結論できる。つまり、背が高いとか血糖値が多いとかを結論として加える。
(2021.06.21, 06.30編集)
検定結果の考え方(復習)
検定結果は前述のように統計では対立仮説(2群に差がある)を正しいとするために、帰無仮説(2群に差がない)の確立を調べ、確立が低いことから帰無仮説を否定し、対立仮説を証明する。(確立について高校の教科書などで確認してください。)
帰無仮説の統計量(2群の平均値/標準誤差)と自由度を用いてt分布表から調べ、危険率が0.05および0.01の水準で、対応する統計量より多いものが優位な統計量となります。(TTEST関数では2群に差がない確率Pが計算され、このP値と0.05または0.01を比較する)
2群に統計的に有意差があれば、もう一度最初の問いに立ち返って、2群のどちらの平均値が大きいか小さいかを見てA群が大きければ、例えば”A群の平均値はB群より大きい”ということがいえます。
基本的な統計に戻る